Поняття лінії визначилося у свідомості людини
в доісторичні часи. Траєкторія кинутого каменя, струмінь води, промені світла,
обриси квітів і листя рослин, звивиста лінія берега річки і моря та інші явища
природи привертали увагу наших предків і, спостережувані багаторазово,
послужили основою для поступового встановлення поняття лінії.
Грецькі вчені створили теорію конічних
перетинів - ліній, що мають особливо велике значення в науці і техніці.
Відкриття їх приписується Менехма (4 століття до н.е.), учневі Евдокса
Кнідського і, як вважають, вчителю Олександра Македонського. Є дані вважати, що Менехм знав властивості
параболи і гіперболи і використовував ці властивості для побудов. На жаль, його
твір з теорії конічних перетинів було загублено. Також не дійшла до нас робота
грецького геометра Аристея, який написав п'ять книг з геометрії, з яких багато
запозичив Евклід для своєї також втраченої роботи по конічних перетинах.
Перша методична обробка конічних перетинів
належить Аполлонію Пергському (3 - 2 ст. До н.е.). Це був трактат «Про конічні
перетини». У своєму трактаті Аполлоній систематизував все, що було відомо до
нього, і відкрив ряд важливих властивостей, встановив їх назви.
В епоху середньовіччя великі досягнення
грецьких вчених були забуті.
До кривим математична наука звернулася тільки в 17
столітті, у зв'язку зі створенням аналітичної геометрії. 1637 - одна з великих
дат в історії математики - рік появи книги Р. Декарта «Геометрія», в якій були
викладені основи методу координат. Відкриття цього методу для дослідження
кривих було фактом першорядного значення. Метод координат не лише створив
загальний, однаковий спосіб символічного завдання кожної кривої у вигляді
відповідного їй рівняння, він давав також необмежену можливість безмежно
збільшувати кількість досліджуваних кривих, оскільки кожне довільно записане
рівняння, що зв'язує між собою дві змінні величини, представляло тепер, взагалі
кажучи, нову криву.
До визначення поняття кривої існувало кілька
підходів.
1.Крива визначається як лінія перетину даної
поверхні площиною, положення якої визначено.
2. Крива визначається як геометричне місце
точок, що володіють даними властивістю.
3. Крива визначається як траєкторія точки,
характер руху якої обумовлений тим чи іншим чином.
Конічні перерізи - плоскі криві, які
одержуємо перетином прямого кругового конуса площиною, яка не проходить через його
вершину. За винятком кількох випадків, конічними перерізами є еліпси, гіперболи
або параболи.
ЕЛІПС
Властивості еліпса у законі руху небесних тіл, відкритому в XVII ст. німецьким астрономом Йоганном
Кеплером : всі планети рухаються навколо
Сонця по орбітах, що мають форму еліпса .
У еліпса є кілька цікавих властивостей, кожну з яких можна використати як
його означення. По-перше, еліпс –
це «сплюснута», а точніше, рівномірно стиснуте до свого діаметра коло.
Сума відстаней від точки еліпса до двох заданих
точок площини (фокусів еліпса) є величиною сталою.
Слово «Focus» в перекладі з латинського означає «вогонь».
Ця назва пішла від цікавої оптичної властивості еліпса: прямі, що з’єднують
любу його точку з фокусами, утворюють з дотичною до еліпса рівні кути.
Якщо уявити собі, що еліпс, як дзеркало, може відбивати світлові промені,
і помістити в один з його фокусів джерело
світла, то промені, відбиваючись від еліпса, зберуться в другому його фокусі.
Таким же чином поширюються і звукові
хвилі, що використовують архітектори для
створення дивовижних звукових ефектів: «балакучі» бюсти, «магічний» шепотіння в
печерах та спорудах, склепіння яких мають еліптичну форму.
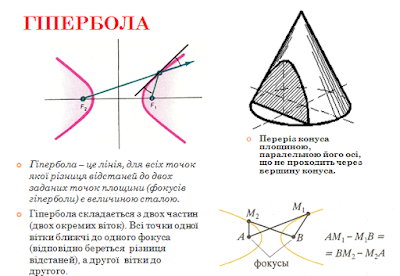
ГІПЕРБОЛА
Переріз
конуса площиною, паралельною його осі, що не проходить через вершину конуса дає
гіперболу.
Гіпербола – це лінія,
для всіх точок якої різниця відстаней до двох заданих точок площини (фокусів
гіперболи) є величиною сталою. Гіпербола складається з двох
частин (двох окремих віток). Всі точки одної вітки ближчі до одного фокуса
(відповідно береться різниця відстаней),
а другої вітки до другого.
Оптична властивість гіперболи: промінь світла, що виходить з одного з фокусів
гіперболи, після відбивання рухається так, ніби він виходить з другого фокуса .
Якщо
виготовити дзеркало вигнувши його по дузі гіперболи, а на прямій, що містить
фокус гіперболи, помістити свічку , то
спостерігач побачить її
відображення в тому ж місці, як при відображенні від плоского дзеркала
ПАРАБОЛА
Параболу можна одержати при перетині конуса
площиною паралельною твірній конуса. Парабола – це крива, що
складається з усіх точок М площини, відстань яких до заданої точки F (фокусу параболи,
дорівнює відстані до заданої прямої L (директриси параболи).
Ближча до директриси точка параболи називається вершиною параболи; пряма,
що проходить через фокус перпендикулярно директрисі, - це вісь симетрії параболи.
Як і інші конічні перерізи, парабола володіє оптичною властивістю: якщо джерело світла помістити в точку F (фокус параболи), то випромінювання буде
відображатися у вигляді пучка паралельних променів .
І
навпаки, промені світла, що падають
паралельно до осі параболи, будуть збиратися в одній точці – в фокусі
параболи.
Переглянути презентацію з теми можна за посиланням
Цікаві криві
























.png)